Principles of Sample Size Calculation
| Site: | EUPATI Open Classroom |
| Course: | Statistics |
| Book: | Principles of Sample Size Calculation |
| Printed by: | Guest user |
| Date: | Wednesday, 9 October 2024, 5:28 PM |
1. Introduction
(This section is organised in the form of a book, please follow the blue arrows to navigate through the book or by following the navigation panel on the right side of the page.)
In a clinical trial, the objective is to obtain information about the effect of a treatment in a certain patient population who are likely to benefit from that treatment. However, the researchers cannot administer this treatment to the entire population. It would not be realistic for ethical, financial and often logistical reasons. Therefore, the clinical trial will be conducted only on a sample from the population of patients. This population sample should be representative of the whole population in order to allow the generalisations of the clinical trial findings.
2. Why Sample Size is Important?
Sample size calculation is the process of determining the appropriate number of participants to include in a clinical trial. The size of the sample should be adequate, allowing statistical analyses to show relevant treatment effects and to generate conclusive results. The larger the number of participants in a trial, the more reliable the conclusions will be. However, larger studies require more resources (both in terms of finances and patient commitment), and may increase the risk for participants to be exposed to inefficient or even unsafe treatment. It is therefore important to optimize the sample size. Moreover, calculating the sample size in the design stage of the study is increasingly becoming a requirement when seeking a favourable ethics committee opinion for a research project.
The wide range of formulas that can be used for specific situations and study designs makes it difficult for most investigators to decide which method to use. The calculation of the sample size is troubled by a large amount of imprecision, because investigators rarely have good estimates of the parameters necessary for the calculation. Unfortunately, the required sample size is very sensitive to the choice of these parameters and small differences in selected parameters can lead to large differences in the sample size
2.1. Components of Sample Size Calculations
greater the variability in the outcome variable (e.g blood pressure) across study population, the larger the sample size required to assess whether an observed effect is a true effect. On the other hand, the more effective (or harmful!) a tested treatment is, the smaller the sample size needed to detect this positive or negative effect. Calculating the sample size for a trial requires five basic components:
Summary of the components for sample size calculations
|
Component |
Definition |
|
Alpha (α) (Type I error) |
The probability of falsely rejecting the null hypothesis (H0) and detecting a statistically significant difference when the groups in reality are not different, i.e. the chance of a false-positive result. |
|
Beta (β) (Type II error) |
The probability of falsely accepting H0 and not detecting a statistically significant difference when a specified difference between the groups exists in reality, i.e. the chance of a false-negative result. |
|
Power (1-β) |
The probability of correctly rejecting H0 and detecting a statistically significant difference when a specified difference between the groups in reality exists. |
|
Minimal clinically relevant difference |
The minimal difference between the groups that the investigator considers biologically plausible and clinically relevant. |
|
Variance |
The variability of the outcome measure, expressed as the Standard Deviation (SD) in case of a continuous outcome. |
Abbreviations: H0 – null hypothesis; the null hypothesis states that compared groups are not different from each other). SD – standard deviation.
2.2. How To Calculate the Sample Size for Randomised Controlled Trials
Formulas for sample size calculation differ depending on the type of study design and the studies outcome(s). These calculations are particularly of interest in the design of randomised controlled trials (RCTs). In general, sample size calculations are
performed based on the primary outcome of the study.
An example of how to calculate sample size using the simplest formulas for an RCT comparing two groups of equal size is given in the following.
Suppose one wished to study the effect of a new hypertensive medicine on systolic blood pressure (SBP) (measured in mmHg) as a continuous outcome.
The simplest formula for a continuous outcome and equal sample sizes in both groups, assuming: α = 0.05 and power = 0.80 (β = 0.20, therefore 1-β=0.8).
n = the sample size in each of the groups
μ1 − μ2 = the difference the investigator wishes to detect
σ2 = population variance (SD)
a = conventional multiplier for alpha* when alpha is 0.05
b = conventional multiplier for power* when beta is 0.80
When the significance level alpha is chosen at 0.05, one should enter the value 1.96 for a in the formula. Similarly, when beta is chosen at 0.20, the value 0.842 should be filled in for b in the formula.
Suppose the investigators consider a difference in SBP of 15 mmHg between the treated and the control group (μ1 – μ2) as clinically relevant, and specified that such an effect should be detected with 80% power (0.80) and a significance level alpha of
0.05. Past experience with similar experiments, with similar measuring methods, and with similar subjects, suggests that the data will be approximately normally distributed with an SD of 20 mmHg. Now we have all of the specifications needed for determining
sample size using the approach as summarized in the formula above.
Entering the values in the formula yields:
This means that a sample size of 28 subjects per group is needed to answer the research question.
*These values are looked up in a statistical table by the researchers. The table values are based on the normal distribution of these errors.
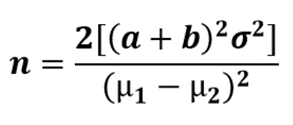
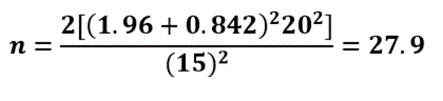
3. Sample vs Population
The key to understanding sample size calculation is to understand the underlying concepts of statistical inference, i.e. using the information from a (random) sample to draw conclusions (inferences) about the population from which the sample was taken.
Analysing the information in a sample will lead to an (observed) estimate for the treatment effect. This should help to predict the true treatment effect in the broader patient population. Every time a sample is taken, by the mere definition of a sample (at least a random one), a different estimate will be obtained. If you looked at several samples together, they will provide a clear picture of the true treatment effect and the variability (i.e. the spread of data, the measure of how far the numbers in a data set are away from the mean or median) underlying the estimation. However, in practice, only one sample is taken, i.e. the trial is run once. So, from the observed effects in samples, what can be determined about the true but unknown treatment effect in the population? This is where statistical inference comes in, more specifically through the concept of hypothesis testing and the use of confidence intervals.
4. Sample Size Calculation
Sample size calculation is an essential part of the design of a clinical trial. The size of the study should be adequate in order to generate conclusive results. Calculating the appropriate sample size requires feedback on various aspects of the trials, such as the study design, the tested hypotheses, the targeted study power and the type I and II errors.5. What Drives a Sample Size Calculation?
There are 5 key drivers in sample size calculations.5.1. The Design of the Clinical Trial
A trial with only one or several experimental treatments arms in a Phase II setting will require a different approach from a randomised comparative Phase III trial. Furthermore, the sample size needed for a study depends on the assumption of the size of the difference expected between the two treatments being studied. In a study where a large difference between the treatments is assumed, the difference should be observable in a smaller sample, whereas a larger sample size is needed to detect a small difference between two treatments. The situation becomes more complex when more than two treatment groups are planned since there is no longer one single clear alternative hypothesis. A test strategy must be defined upfront and adequate measures applied to maintain the overall type I error.5.2. The Choice of the Primary Endpoint(s)
Endpoints in clinical research are the outcomes measured during the study that are used to assess the efficacy of the treatment. They can be of different types:
- Binary vs. continuous: binary indicates whether an event has occurred (occurrence or relief of symptoms), while continuous represents a specific measure or count (e.g., blood pressure).
- Landmark: its goal is to have a fixed time (time-to-event) after the initiation of the treatment, where analysis of survival can be conducted.